Regression beschreibt die Beziehung zwischen einer abhängigen Variablen (der Wert der vorausgesagt werden soll – Ziel variable) und einer oder mehreren unabhängigen Variablen (die Werte, auf welche die Voraussagen beruhen – Merkmals variable).
Die einfachsten Formen der Regression nehmen an, dass die Beziehung zwischen abhängiger und unabhängiger Variablen einer geraden Linie folgen.
Ich möchte auf dieser Seite zwei Beispiele präsentieren, wie sich durch die Anwendung der linearen Regression, die Lebenserwartung verschiedener Länder prognostizieren lässt und im anderen Beispiel die Preise für Getriebe vorausgesagt werden können – oder auch nicht (mehr dazu erfahren Sie weiter unten).
Wir verwenden für das erste Beispiel den sehr bekannten gapminder Datensatz. Weitere Informationen zu gapminder findet man hier:
www.gapminder.org
Für das zweite Beispiel werden Preise von Getrieben bereitgestellt, sowie deren jeweiligen Gewichte. Das Beispiel zeigt die möglichen Schritte bei einem machine learning projekt und ob sich die Hypothese, dass es eine Abhängigkeit zwischen Preis und Gewicht gibt, bestätigen lässt.
Das Erste Beispiel – Lebenserwartung
Nach Anwendung der linearen Regression – Lebenserwartung in Abhängigkeit von Kalenderjahren – können folgende statistische Werte ermittelt werden:
Call:
lm(formula = lifeExp ~ year, data = .x)
Residuals:
Min 1Q Median 3Q Max
-0.84179 -0.18398 -0.00942 0.22152 0.59504
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.495e+02 1.378e+01 -25.37 2.07e-10 ***
year 2.137e-01 6.959e-03 30.71 3.15e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4161 on 10 degrees of freedom
Multiple R-squared: 0.9895, Adjusted R-squared: 0.9885
F-statistic: 942.9 on 1 and 10 DF, p-value: 3.146e-11 term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -350. 13.8 -25.4 2.07e-10
2 year 0.214 0.00696 30.7 3.15e-11
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual
* <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <int>
1 0.990 0.988 0.416 943. 3.15e-11 2 -5.41 16.8 18.3 1.73 10Die oben genannten statistischen Werte beziehen sich alle auf Deutschland. Die recht kompliziert wirkende lineare model lässt sich sehr schon visuell darstellen (Bitte auf das Bild klicken für eine größere Darstellung):
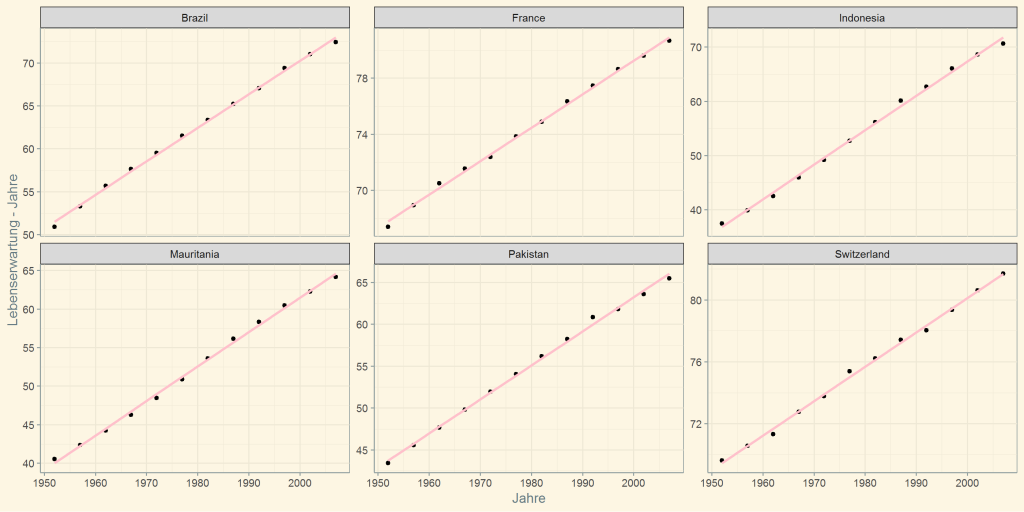
Wir haben hier die Länder hervorgehoben, bei denen die lineare Regression sehr gute Ergebnisse liefert und sich mit einer sehr hohen Wahrscheinlichkeit sinnvolle Zukunftsprognosen ermitteln lassen.
Zweites Beispiel – Getriebe Preise
Wir werden bei diesem Beispiel den Python Code mit abbilden. In diesem kleinen Projekt bekommt mab eine kleine Einsicht, wie Datenwissenschaftler Vorgehen bei der Analyse und Verbesserung von Modellen.
Als ersten Schritt werden wir die notwendigen Python Bibliotheken laden, sowie die notwendigen Daten. Die Nachkommastellen werden noch richtig gestellt.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_excel("data.xlsx")
data["Preis"] = np.round_(data["Preis"],decimals=2)
data["Preis Währungsumrechnung"] = np.round_(data["Preis Währungsumrechnung"],decimals=2)Um die Daten besser zu verstehen, führen wir eine explorative Datenanalyse (EDA) durch. Die EDA unterstütz im Erkennen wichtiger Merkmale, die für das spätere Regressionsmodell wichtig sind oder sein können.
Zum Start werden wir Standard Python Funktionen verwenden um ein besseres Verständnis für die Daten zu bekommen.
data.head()
data.info()
data.describe()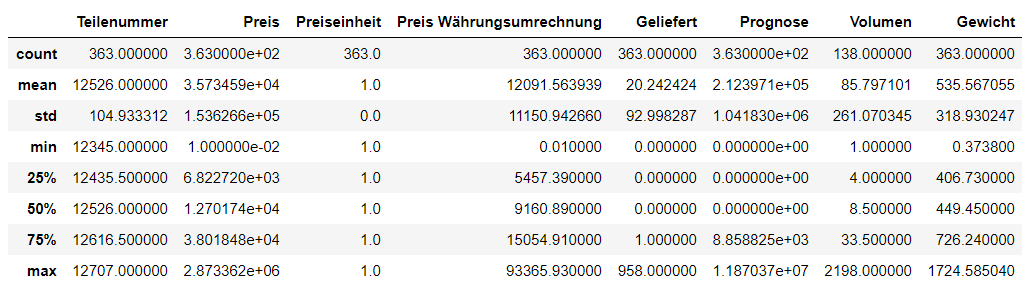
Nachdem die Daten numerisch untersucht wurden, werden Sie visuell untersucht.
import matplotlib.pyplot as plt
data.hist(bins=50,figsize=(20,15))
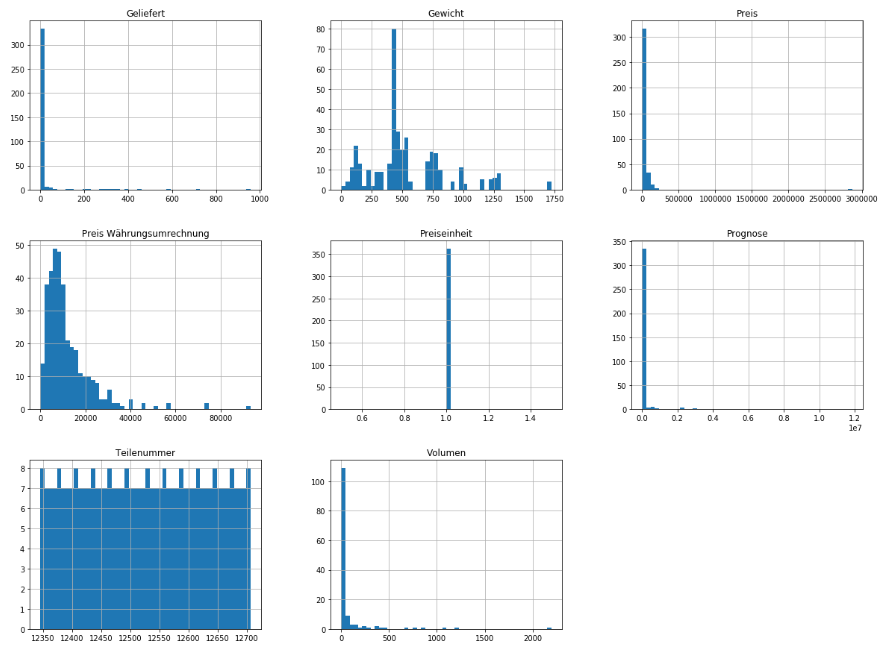
Die Visuelle Datenanalyse zeigt das es bei einigen Werten Ausreißer gibt, bzw. das innerhalb der Daten eine starke Streuung vorhanden ist.
Ausreißer lassen sich sehr gut mit Boxplots näher untersuchen. Wir verwenden unten eine weitere Analyse der Gewichte und Preise mit Boxplots.
data[["Gewicht"]].boxplot(figsize=(10,5),vert=False)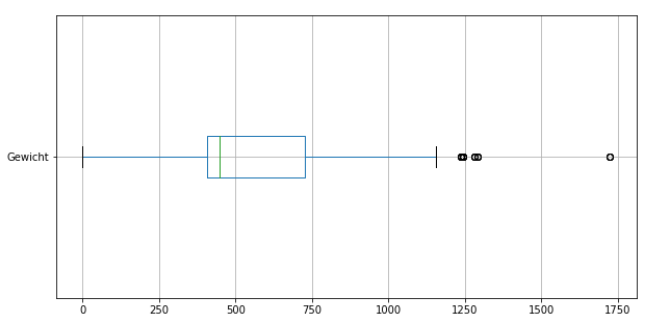
data[["Preis"]].boxplot(figsize=(10,5),vert=False)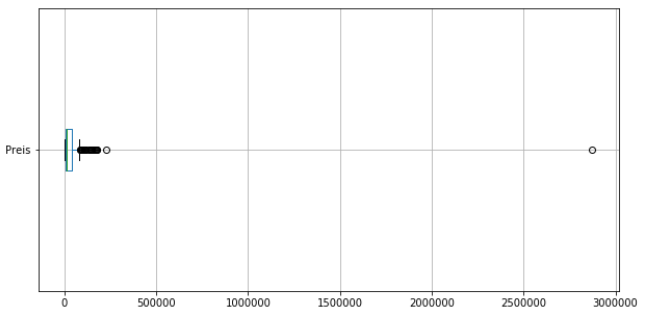
data[["Preis Währungsumrechnung"]].boxplot(figsize=(10,5),vert=False)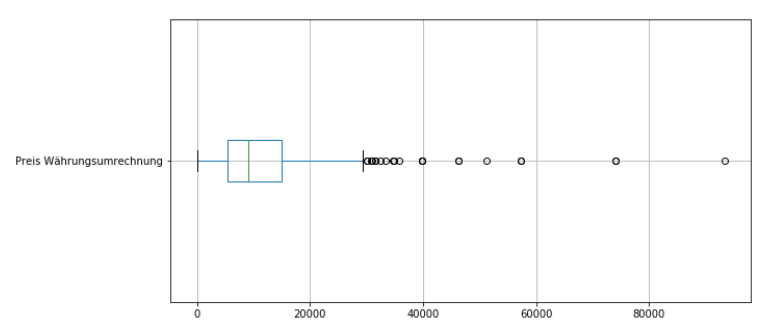
Die Boxplots zeigen bereits, dass die Daten sehr stark streuen. Das sind bereits jetzt erste Anzeichen dafür, dass die Daten nicht linear verteilt sind und ein lineares Regressionsmodel schnell an seine Grenzen kommen wird.
Im nächsten Schritt werden wir anfangen unser Model zu erstellen. Als erstes erstellen wir die Merkmals- und Ziel variable. Nach der Erstellung werden die Daten noch einem „reshape“ unterzogen um sie in das für scikit-learn richtige Format zu bringen.
y = data["Preis Währungsumrechnung"].values
X = data["Gewicht"].values
y = y.reshape(-1,1)
X = X.reshape(-1,1)
Wir werden jetzt die Daten auf Korrelation untersuchen. Dazu erstellen wir eine Korrelationsmatrix. Wir werden die Korrelation auch graphisch abbilden unter Verwendung von Streudiagramm und einer Heatmap. Die Heatmap erstellen wir mit Hilfe der Bibliothek seaborn.
corr_matrix = data.corr()
corr_matrix.head()
corr_matrix["Preis"].sort_values(ascending=False)
Preis 1.000000
Gewicht 0.251998
Preis Währungsumrechnung 0.169120
Teilenummer 0.162503
Prognose 0.023950
Volumen 0.020046
Geliefert 0.017034
Preiseinheit NaN
Name: Preis, dtype: float64<br><br></pre>
Die Korrelationsmatrix zeigt insgesamt sehr schwache (bis unbrauchbare) Korrelationen. Die Korrelationswerte werden besser wenn man die Preise verwendete welche bereits eine Währungsumrechnung hinter sich haben.
corr_matrix = data.corr()
corr_matrix.head()
corr_matrix["Preis Währungsumrechnung"].sort_values(ascending=False) Preis Währungsumrechnung 1.000000
Gewicht 0.516758
Teilenummer 0.468088
Preis 0.169120
Prognose -0.036587
Volumen -0.055725
Geliefert -0.060050
Preiseinheit NaN
Name: Preis Währungsumrechnung, dtype: float64Weiter unten erstellen wir die Streudiagramme und die Heatmap:
from pandas.plotting import scatter_matrix
attributes=["Gewicht","Preis","Teilenummer","Volumen"]
scatter_matrix(data[attributes],figsize=(15,10))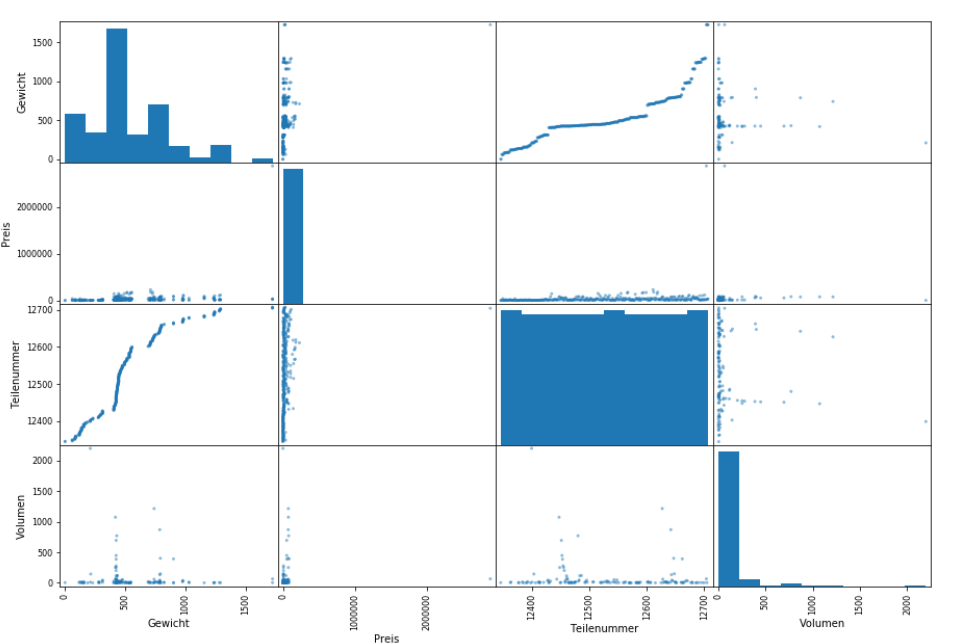
%matplotlib inline
import seaborn as sns
sns.heatmap(data.corr(), square=True, cmap='RdYlGn')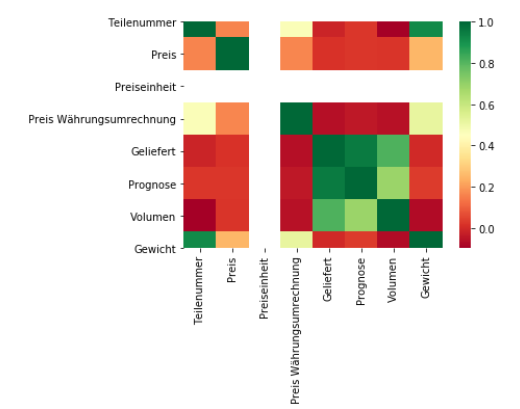
In der Heatmap erkennt man eine Korrelation von ca. 0.5 zwischen den Variablen Gewicht und Preis Währungsumrechnung.
Jetzt ist es an der Zeit das Regression Model zu bauen und graphisch abzubilden und numerisch zu analysieren.
Das Regression Model wird mit den folgenden Code erstellt:
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
prediction_space = np.linspace(min(X), max(X)).reshape(-1,1)
reg.fit(X,y)
y_pred = reg.predict(prediction_space)
Die Graphische Abbildung wird mit folgendem Code erstellt:
data.plot(kind="scatter", x="Gewicht", y="Preis Währungsumrechnung", alpha=0.5)
plt.plot(prediction_space,y_pred, color='black', linewidth=3)
plt.show()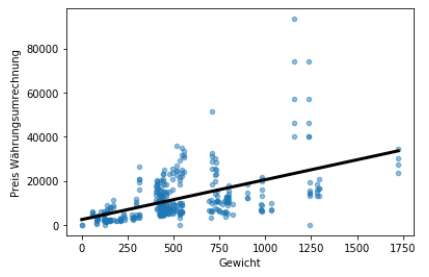
Das Model kommt auf folgenden „score“:
print(reg.score(X, y))
0.2670388471450631 Das Ergebnis ist hier eher ernüchternd. Das Model wird so nicht viel Mehrwert bei einer Preisanalyse bieten.
Zur Verbesserung des Models möchten wir zwei weitere Möglichkeiten untersuchen. Der erste Ansatz ist die Ausreißer aus dem Model zu beseitigen und die Daten in verwandte Gruppen zu unterteilen. Dazu verwenden wir die K-Means Cluster Methode. Die zweite Möglichkeit ist ein Regressionsmodell zu verwenden, welches mit nicht linearen variablen arbeiten kann.
Mit folgendem Code werden als erstes eine Sinnvoll Anzahl von Clustern festgelegt und danach visuell abgebildet. Wir verwenden für die automatische Festlegung der Cluster Anzahl die Ellenbogen Methode.
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
df = pd.DataFrame({
'x': data["Gewicht"],
'y': data["Preis Währungsumrechnung"]
})
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans.fit(df)
wcss.append(kmeans.inertia_)
plt.plot(range(1, 11), wcss)
plt.title('Elbogen Method')
plt.xlabel('Anzahl Clusters')
plt.ylabel('WCSS')
plt.show()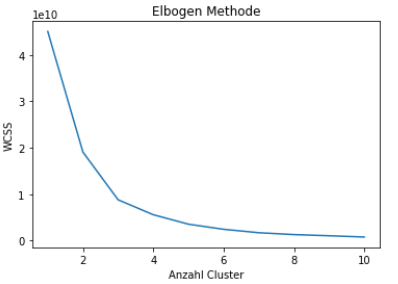
kmeans = KMeans(n_clusters=4, init='k-means++', max_iter=300, n_init=10, random_state=0)
pred_y = kmeans.fit_predict(df)
data.plot(kind="scatter", x="Gewicht", y="Preis Währungsumrechnung", alpha=0.3,c=pred_y,cmap="viridis")
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red')
plt.show()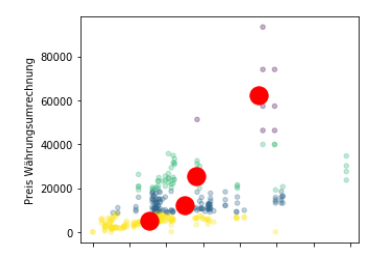
Nach der Darstellung der Cluster eröffnet sich jetzt die Möglichkeit Regressionsmodelle für die jeweiligen Cluster zu erstellen, mit der Intention Modelle mit einer besseren Vorhersehbarkeit zu erstellen.
Zusammenfassend kann man sagen, das die Lineare Regression ein grundlegendes statistisches Modell in der Datenanalyse ist, das verwendet wird, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu untersuchen. Der Hauptvorteil der linearen Regression besteht darin, dass sie ein einfaches und leicht interpretierbares Modell bietet, das Vorhersagen und Trendanalysen ermöglicht. Ein weiterer Vorteil ist ihre Effizienz in der Berechnung, was sie ideal für Situationen macht, in denen schnelle Analysen erforderlich sind.
Ein Nachteil der linearen Regression ist ihre Beschränkung auf lineare Beziehungen, was bedeutet, dass sie nicht effektiv ist, wenn die Datenbeziehungen komplex oder nicht-linear sind. Zudem kann das Modell durch Ausreißer und Multikollinearität (hohe Korrelation zwischen unabhängigen Variablen) beeinträchtigt werden, was die Genauigkeit der Vorhersagen reduzieren kann. Daher ist es wichtig, die Daten sorgfältig auf solche Probleme zu prüfen, bevor man sich auf das Modell verlässt.
