In diesem Artikel möchten ich kurz die Hierarchische Clusteranalyse vorstellen.
Ist gibt zwei grundsätzliche Verfahren für die Hierarchische Clusteranalyse. Man nennt sie Top-Down und Bottom-Up Verfahren.
Die Top-Down Verfahren werden als divisive Cluster-verfahren bezeichnet. Im englischen Sprachgebrauch wird hierfür gerne die Abkürzung DIANA verwendet. Sie steht für Divise Analysis.
Wir steigen gleich ein, indem wir die notwendigen Bibliotheken laden:
library(tidyverse) # data manipulation
library(cluster) # clustering algorithms
library(factoextra) # clustering visualization
library(gapminder)Verwendet wird in meinem Beispiel der bekannte gapminder Datensatz. Wir haben diesen bereits mit library(gapminder) geladen.
Betrachten wir den Datensatz mit der funktion head().
head()
A tibble: 6 x 6
country continent year lifeExp pop gdpPercap
1 Afghanistan Asia 1952 28.8 8425333 779.
2 Afghanistan Asia 1957 30.3 9240934 821.
3 Afghanistan Asia 1962 32.0 10267083 853.
4 Afghanistan Asia 1967 34.0 11537966 836.
5 Afghanistan Asia 1972 36.1 13079460 740.
6 Afghanistan Asia 1977 38.4 14880372 786.Der gapminder Datensatz zeigt die Entwicklungen der einzelnen Länder pro Jahr. Da wir Länder untereinander vergleichen möchten, werden wir mit Durchschnittswerten arbeiten. Diese erzeugen wir mit folgenden Code:
df <- gapminder %>%
group_by(country) %>%
summarise(lifeExp_mean = mean(lifeExp),
pop_mean = mean(pop),
gdpPercap_mean = mean(gdpPercap)) %>%
filter(lifeExp_mean < 50) %>%
na.omit()
head(df)
A tibble: 6 x 4
country lifeExp_mean pop_mean gdpPercap_mean
1 Afghanistan 37.5 15823715. 803.
2 Albania 68.4 2580249. 3255.
3 Algeria 59.0 19875406. 4426.
4 Angola 37.9 7309390. 3607.
5 Argentina 69.1 28602240. 8956.
6 Australia 74.7 14649312. 19981.Mit den nächsten Schritten werden wir die Daten anpassen, damit man eine Hierarchische Clusteranalyse durchführen kann. Zu Beginn werden wir die erste Spalte umwandeln, damit diese als Reihen namen erkannt wird.
df <- column_to_rownames(df,"country")
head(df)
lifeExp_mean pop_mean gdpPercap_mean
Afghanistan 37.47883 15823715 802.6746
Albania 68.43292 2580249 3255.3666
Algeria 59.03017 19875406 4426.0260
Angola 37.88350 7309390 3607.1005
Argentina 69.06042 28602240 8955.5538
Australia 74.66292 14649313 19980.5956Danach folgt die Skalierung/Standardisierung der Daten mit scale().
df <- scale(df)
d <- dist(df, method = "euclidean")
head(d)Nachdem die Skalierung / Standardisierung abgeschlossen ist, werden die Daten auf Unterschiede untersucht, bzw. es wird eine Distanzmatrix erstellt. Wir verwenden in unserem Beispiel den häufig verwendeten euklidischen Abstand. Wir haben die dist() funktion bereits oben ausgeführt.
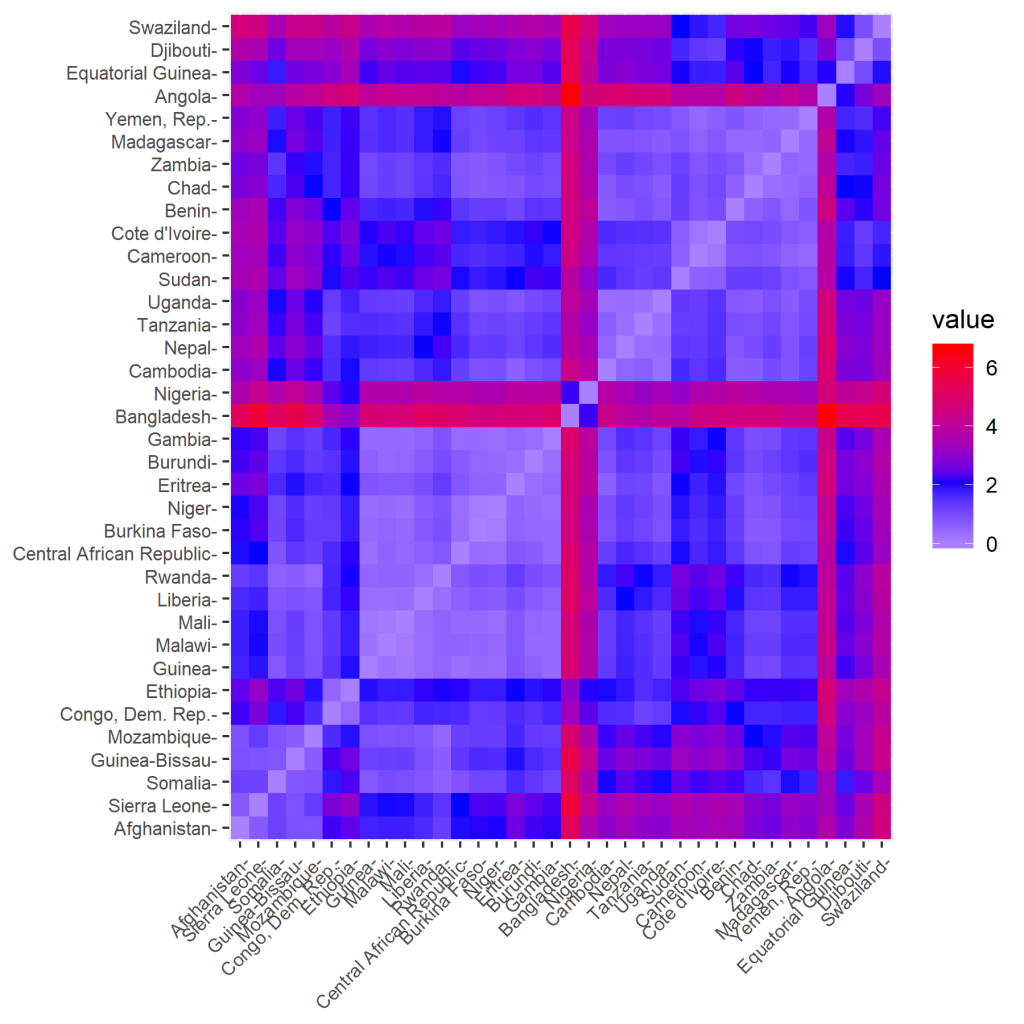
Die Distanzmatrix lässt sich auch bildlich darstellen. Wir verwenden dazu folgende Code:
fviz_dist(d, gradient = list(low = "white", mid = "blue", high = "red"))Dadurch erhält man folgende Distanzmatrix als Bild:
Jetzt führen wir die Berechnung der Cluster durch. Dazu verwenden wir die „complete“ Methode.
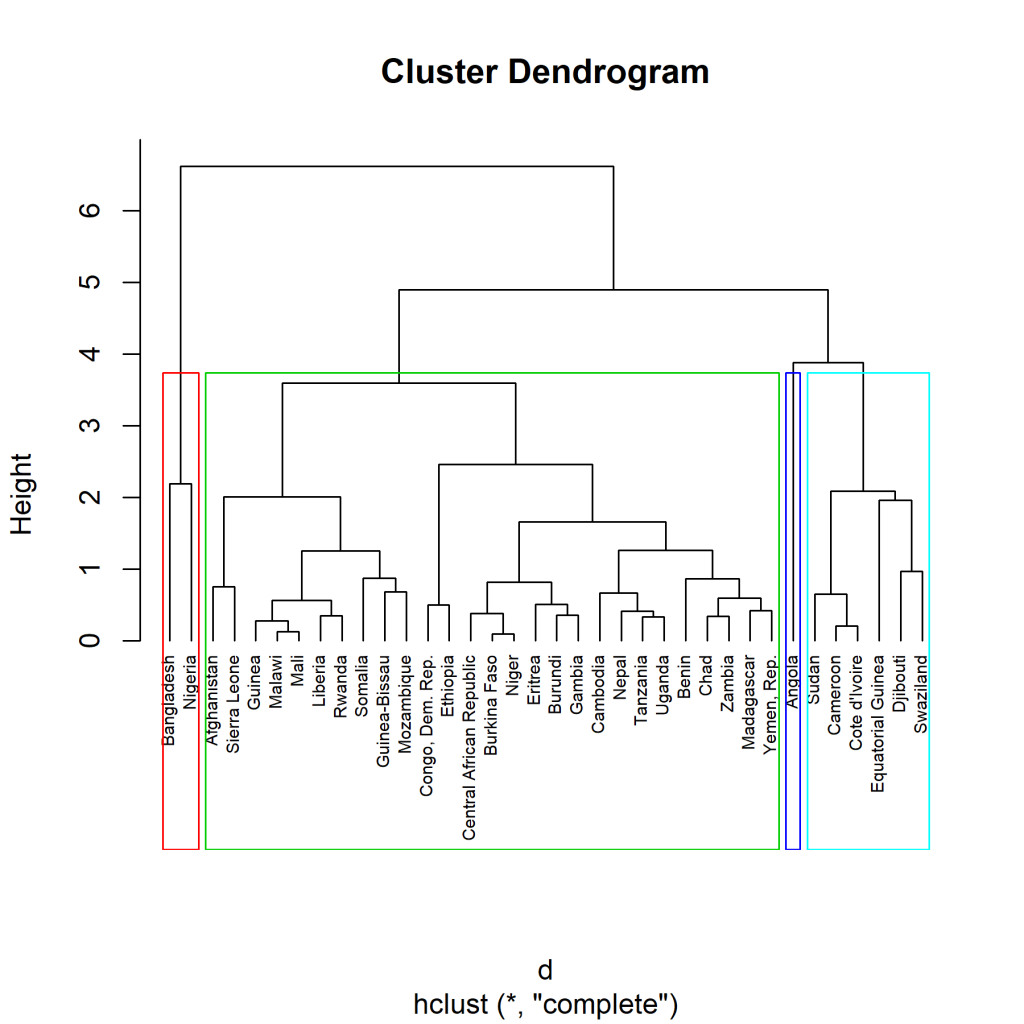
hc1 <- hclust(d, method = "complete" )
plot(hc1, cex = 0.6, hang = -1)
rect.hclust(hc1, k = 4, border = 2:6)Mit der Funktion rect.hclust() haben wir die Cluster noch farblich in Quadrate eingeteilt.
Eine weitere Möglichkeit ist der Verwendung des factoextra Packetes. Wie führen den folgenden Code aus um das Paket zu verwenden:
hc.cut <- hcut(d, k = 4, hc_method = "complete")
fviz_dend(hc.cut, show_labels = TRUE, rect = TRUE)
fviz_cluster(data=d,hc.cut, frame.type = "convex")Erstell wird dadurch ein weiteres Dendrogramm und ein weitere Darstellung der Cluster.
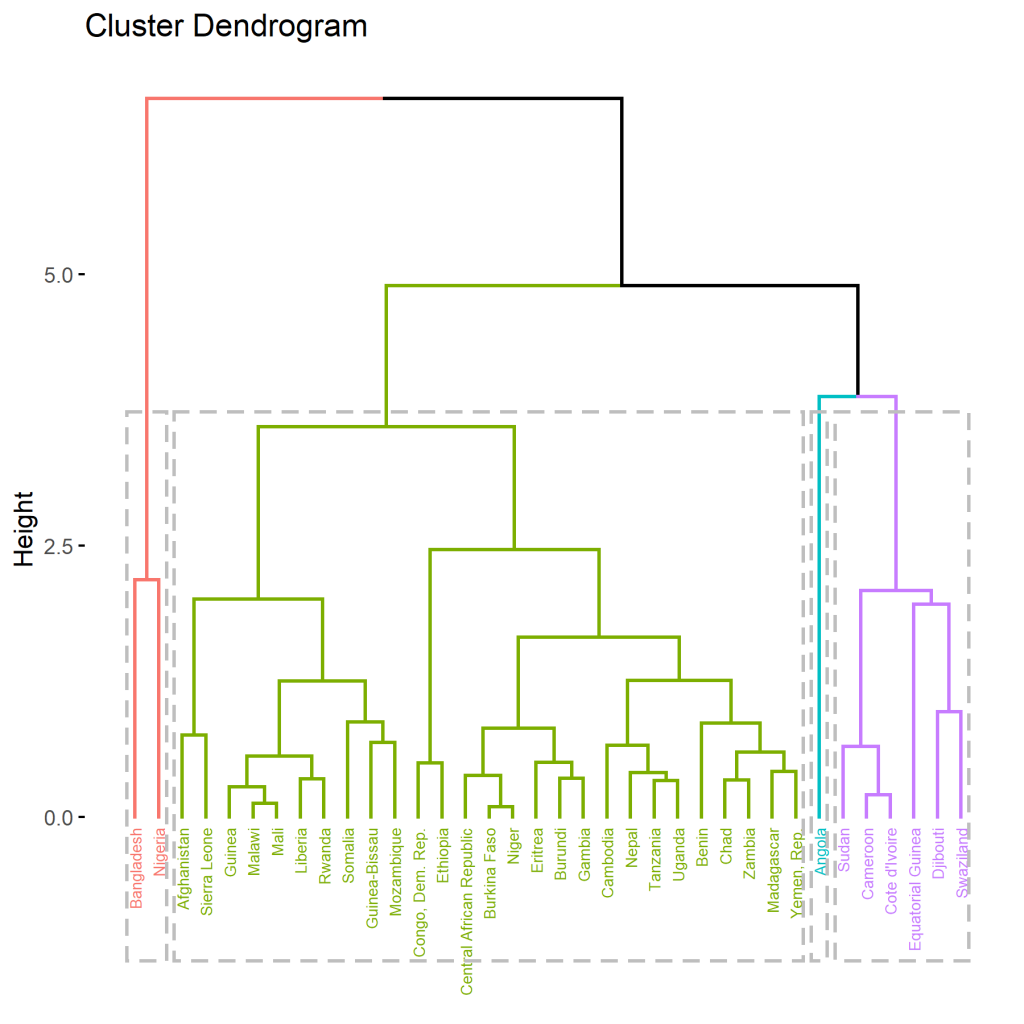
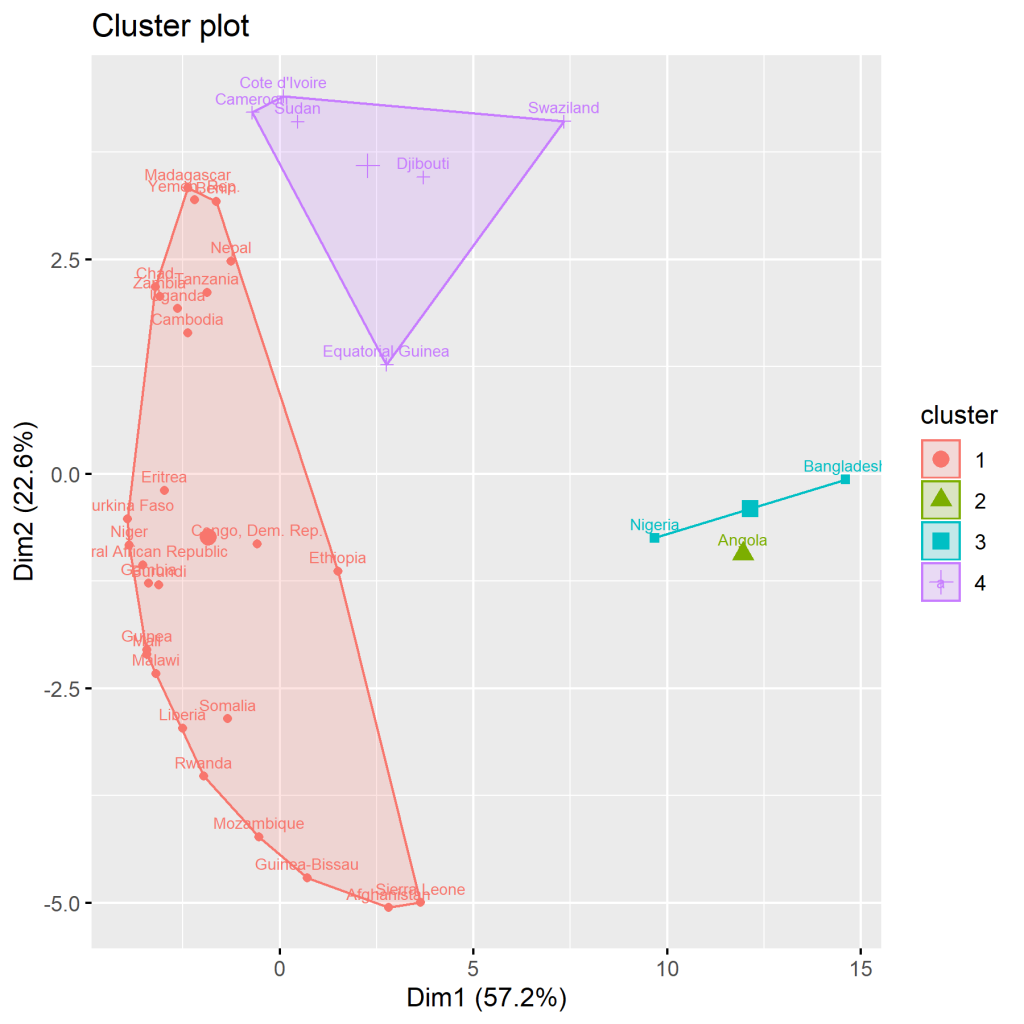
Cluster Plots und die hierarchische Clusteranalyse sind mächtige Werkzeuge in der Welt der Datenanalyse, insbesondere nützlich für Aufgaben in Supply Chain Management und Operations Management. Sie helfen, die komplexen Strukturen und Beziehungen innerhalb großer Datensätze zu entwirren und bieten eine visuelle Darstellung von Gruppierungen oder Clustern innerhalb dieser Daten. Hier ein detaillierter Einblick in ihre Anwendungsbereiche:
Erkennung natürlicher Gruppierungen
Die hierarchische Clusteranalyse ermöglicht es uns, natürliche Gruppierungen innerhalb eines Datensatzes zu identifizieren. Zum Beispiel können Kunden eines Online-Einzelhändlers basierend auf Kaufverhalten, Präferenzen und demografischen Merkmalen in verschiedene Gruppen eingeteilt werden. Dieses Wissen ermöglicht es Unternehmen, maßgeschneiderte Marketingstrategien zu entwickeln, die auf spezifische Kundensegmente abzielen.
Optimierung von Lieferketten
In der Lieferkettenverwaltung kann die hierarchische Clusteranalyse dazu beitragen, Lieferanten oder Transportwege zu clustern, die ähnliche Eigenschaften aufweisen, wie geographische Nähe oder Lieferfähigkeiten. Durch die Analyse dieser Cluster können Unternehmen effizientere Routen planen, Transportkosten senken und die Lieferzeit verkürzen.
Verbesserung der betrieblichen Effizienz
Die Clusteranalyse kann auch dazu verwendet werden, Produktionsprozesse zu optimieren. Durch die Gruppierung von Maschinen, die ähnliche Aufgaben ausführen oder ähnliche Wartungsbedürfnisse haben, können Betriebsleiter Wartungspläne effizienter gestalten und Ausfallzeiten minimieren.
Entscheidungsfindung und Strategieentwicklung
Die visuelle Darstellung in Cluster Plots ermöglicht es Führungskräften, die Struktur der Daten schnell zu erfassen und fundierte Entscheidungen zu treffen. In einem Cluster Plot dargestellte Daten können Aufschluss darüber geben, welche Geschäftsbereiche verstärkt Aufmerksamkeit benötigen oder welche Strategien angepasst werden sollten, um die Leistung zu verbessern.
Risikomanagement
Durch die Identifizierung von Clustern, die ein hohes Risiko darstellen könnten, wie z.B. Cluster von Lieferanten in politisch instabilen Regionen, können Unternehmen proaktive Maßnahmen ergreifen, um potenzielle Unterbrechungen in der Lieferkette zu vermeiden.
Fazit
Cluster Plots und die hierarchische Clusteranalyse sind nicht nur Werkzeuge für Datenwissenschaftler, sondern auch unentbehrliche Instrumente für jeden, der in den Bereichen Supply Chain und Operations Management tätig ist. Sie bieten tiefe Einblicke und fördern datengestützte Entscheidungen, die essentiell für die Wettbewerbsfähigkeit und Effizienz in der modernen Geschäftswelt sind. Durch ihre Fähigkeit, komplexe Datenmengen zugänglich und interpretierbar zu machen, spielen sie eine Schlüsselrolle bei der Transformation von Daten in handlungsreiche Erkenntnisse.
