Die Zusammenhänge lassen sich graphisch durch eine Korrelationsmatrix oder Streudiagramm darstellen.
Wir verwenden hier das corrgram package.
Bevor man eine Regression erstellt, ist es oft sinnvoll zu analysieren, wie die unabhängigen und abhängigen Variablen zueinander in Beziehung stehen.
Zu Beginn werden wir die Libraries laden und auch den Datensatz mit welchem wir arbeiten möchten:
library(gapminder)
library(tidyverse) # Das Schweizer Messer für Daten Manipulation
library(corrgram)
Nachdem man corrgram geladen hat, kann man mit der funktion cor() bereits eine erste Korrelationsmatrix erstellen. Wir verwenden als Beispiel den berühmt, berüchtigten mtcars Datensatz. Dieser ist bei jeder R installation bereits integriert.
options(digits = 2)
cor(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
mpg 1.00 -0.85 -0.85 -0.78 0.681 -0.87 0.419 0.66 0.600 0.48 -0.551
cyl -0.85 1.00 0.90 0.83 -0.700 0.78 -0.591 -0.81 -0.523 -0.49 0.527
disp -0.85 0.90 1.00 0.79 -0.710 0.89 -0.434 -0.71 -0.591 -0.56 0.395
hp -0.78 0.83 0.79 1.00 -0.449 0.66 -0.708 -0.72 -0.243 -0.13 0.750
drat 0.68 -0.70 -0.71 -0.45 1.000 -0.71 0.091 0.44 0.713 0.70 -0.091
wt -0.87 0.78 0.89 0.66 -0.712 1.00 -0.175 -0.55 -0.692 -0.58 0.428
qsec 0.42 -0.59 -0.43 -0.71 0.091 -0.17 1.000 0.74 -0.230 -0.21 -0.656
vs 0.66 -0.81 -0.71 -0.72 0.440 -0.55 0.745 1.00 0.168 0.21 -0.570
am 0.60 -0.52 -0.59 -0.24 0.713 -0.69 -0.230 0.17 1.000 0.79 0.058
gear 0.48 -0.49 -0.56 -0.13 0.700 -0.58 -0.213 0.21 0.794 1.00 0.274
carb -0.55 0.53 0.39 0.75 -0.091 0.43 -0.656 -0.57 0.058 0.27 1.000
Wir haben mit der Funktion options(digits=2) die nachkommastellen auf 2 reduziert. Dies hilft für eine bessere Darstellung der Daten. Man sieht das die Korrelationsmatrix ein sehr mächtiges Tool ist, aber den Nachteil hat, dass größere Datensätze schnell unübersichtlich werden können!
Deshalb ist es immer sinnvoll die Abhängigkeiten visuell darzustellen.
Wir werden jetzt zum gapminder Datensatz wechseln. Es ist wichtig das alle Daten welche für die Korrelationsmatrix verwendet werden, numerich sind. Eine Überprüfung des gapminder Datensatzes zeigt ein Problem
str(gapminder) Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 1704 obs. of 6 variables: $ country : Factor w/ 142 levels "Afghanistan",..: 1 1 1 1 1 1 1 1 1 1 … $ continent: Factor w/ 5 levels "Africa","Americas",..: 3 3 3 3 3 3 3 3 3 $ year : int 1952 1957 1962 1967 1972 1977 1982 1987 1992 1997 … $ lifeExp : num 28.8 30.3 32 34 36.1 … $ pop : int $ gdpPercap: num 779 821 853 836 740 …
Es befinden sich die Datentypen „Factor“ im Datensatz. Diese müssen aus dem Datensatz entfernt werden. Als erstes möchten wir aber auch die Durchschnittswerte von lifeExp und gdpPercap per Land ermitteln.
data_grouped <- gapminder %>%
group_by(country) %>%
summarise(lifeExp_mean = mean(lifeExp),
gdpPercap_mean = mean (gdpPercap),
pop_mean = mean(pop))
Durch den Einsatz von tidyverse tools konnte wir die Durchschnittwerte der Lebenswertung und Einkommen pro Land ermitteln. Die Daten sind jetzt pro Land. Nach überprüfen haben wir das Factor Problem aber noch nicht gelöst:
head(data_grouped)
A tibble: 6 x 4
country lifeExp_mean gdpPercap_mean pop_mean
1 Afghanistan 37.5 803. 15823715.
2 Albania 68.4 3255. 2580249.
3 Algeria 59.0 4426. 19875406.
4 Angola 37.9 3607. 7309390.
5 Argentina 69.1 8956. 28602240.
6 Australia 74.7 19981. 14649312.
str(data_grouped)
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 142 obs. of 4 variables:
$ country : Factor w/ 142 levels "Afghanistan",..: 1 2 3 4 5 6 7 8
$ lifeExp_mean : num 37.5 68.4 59 37.9 69.1 …
$ gdpPercap_mean: num 803 3255 4426 3607 8956 …
$ pop_mean : num 15823715 2580249 19875406 7309390 28602240 …
Der Lösungsansatz ist die column_to_rownames Funktion. Diese Funktion sollte sich gerade neue R user gut merken, da Sie viele Stunden suche auf stackoverflow ersparen kann!
data_grouped <- column_to_rownames(data_grouped,"country")
head(data_grouped)
lifeExp_mean gdpPercap_mean pop_mean
Afghanistan 37 803 1.6e+07
Albania 68 3255 2.6e+06
Algeria 59 4426 2.0e+07
Angola 38 3607 7.3e+06
Argentina 69 8956 2.9e+07
Australia 75 19981 1.5e+07
str(data_grouped)
'data.frame': 142 obs. of 3 variables:
$ lifeExp_mean : num 37.5 68.4 59 37.9 69.1 …
$ gdpPercap_mean: num 803 3255 4426 3607 8956 …
$ pop_mean : num 15823715 2580249 19875406 7309390 28602240 …
Nach Überprüfung mit der Funktion str() erkennt man, dass die Daten jetzt im Format „data.frame“ sind und nur aus numerischen Daten bestehen.
Die informationen über die Länder sind aber noch enthalten, auch wenn diese mit str() nicht angezeigt werden. Mit head() lassen sich die Länder mit abrufen.
Jetzt können wir die Korrelationsmatrix aufrufen.
cor(data_grouped)
lifeExp_mean gdpPercap_mean pop_mean
lifeExp_mean 1.000 0.675 0.021
gdpPercap_mean 0.675 1.000 -0.047
pop_mean 0.021 -0.047 1.000
Aus der Tabelle lassen sich eine Abhängigkeit zwischen gdpPercap_mean und lifeExp_mean erkennen. Höheres BIP pro Kopf (Gross Domestic Product per capita) trägt zu einer höheren Lebenserwartung (Liefe Expectancy) bei!
Jetzt erstellen wir eine visuelle Korrelationsmatrix mit Hilfe von corrgram.
corrgram(data_grouped, order=TRUE, lower.panel=panel.pts,
upper.panel=panel.pie, text.panel=panel.txt,
main="Correlogram gapminder")
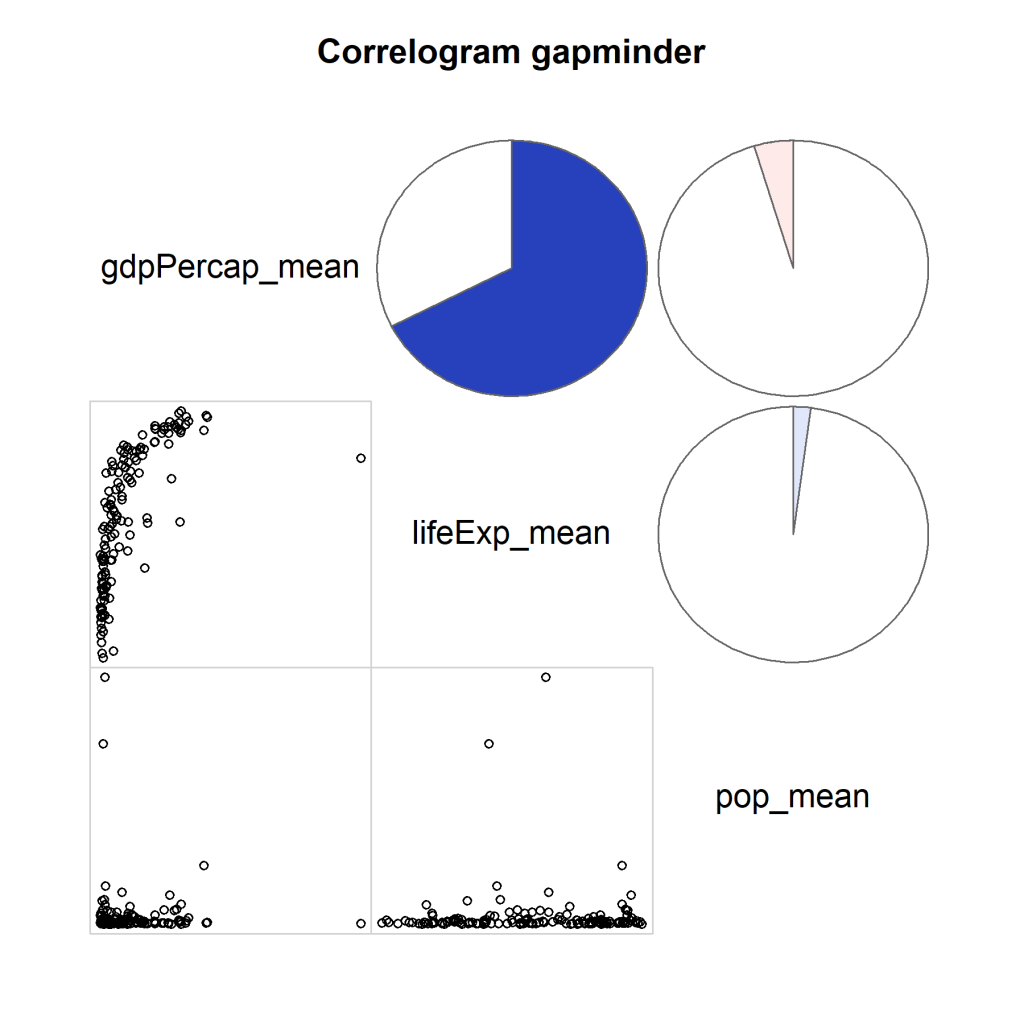
Wir haben durch die Verwendung des von uns weiter vereinfachten gapminder datensatz einen Datensatz erschaffen, bei dem die stärken der Visualisierung nicht unbedingt gezeigt werden (erkennen von Muster in komplexen Datensätze). Deshalb folgt unten noch ein Beispiel mit dem mtcars Datensatz. Hier sind die Vorteile einer Visualisierung schnell zu erkennen.
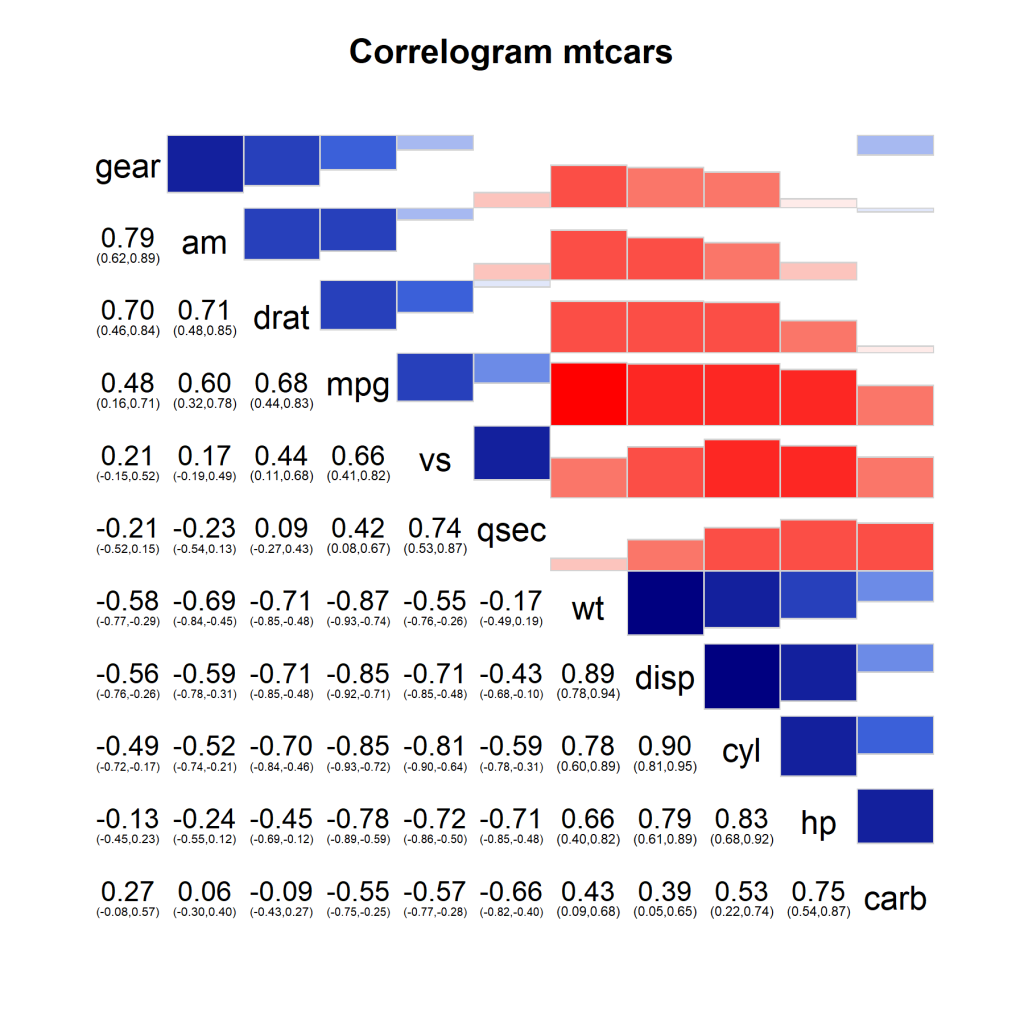
corrgram(mtcars, order=TRUE, lower.panel=panel.conf,
upper.panel=panel.bar, text.panel=panel.txt,
main="Correlogram mtcars")
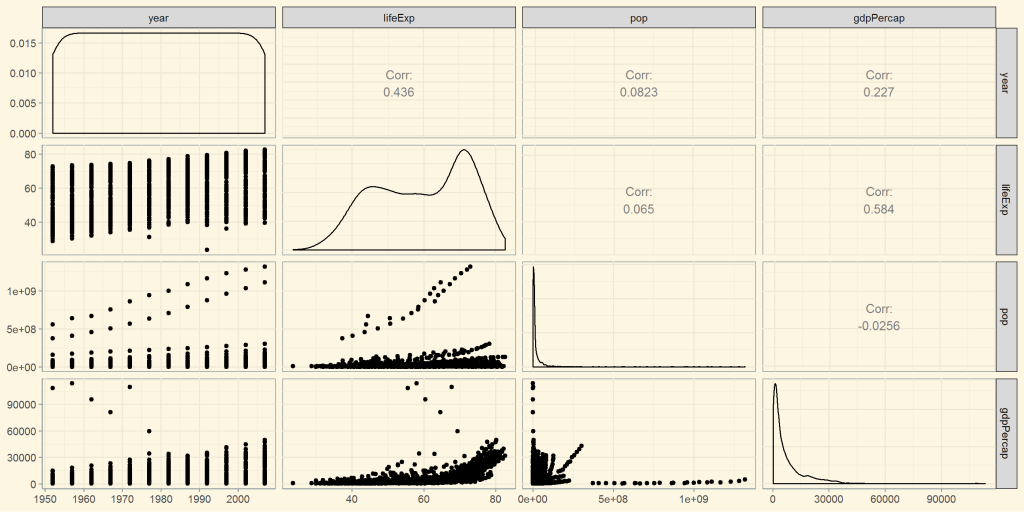
Anbei folgen Beispiele einer Streudiagramm Matrix (Scatterplot Matrix, oft auch als „SPLOM“ bezeichnet). Bitte klicken Sie auf die Bilder für eine größere Darstellung:
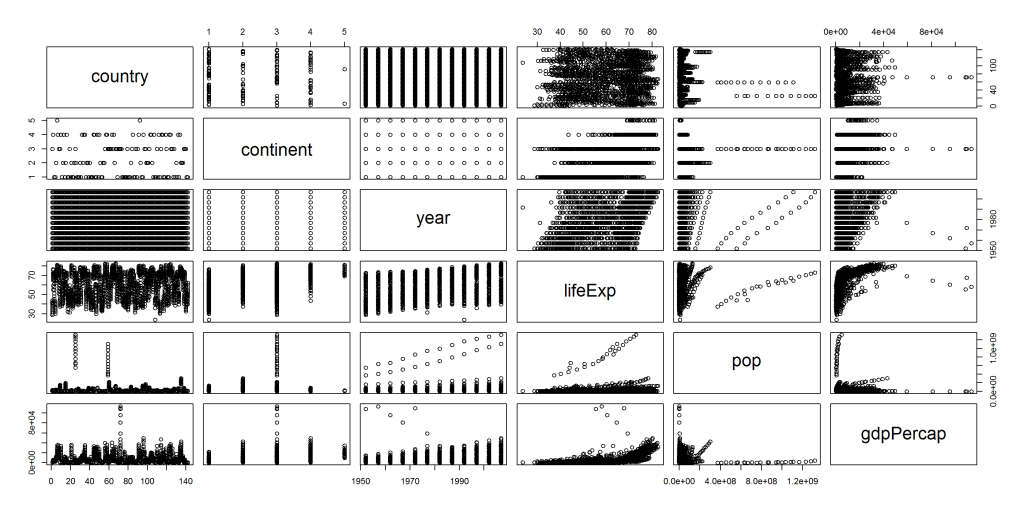
SPLOM mit numerischer Darstellung und Density Plots (Dichtediagramm):
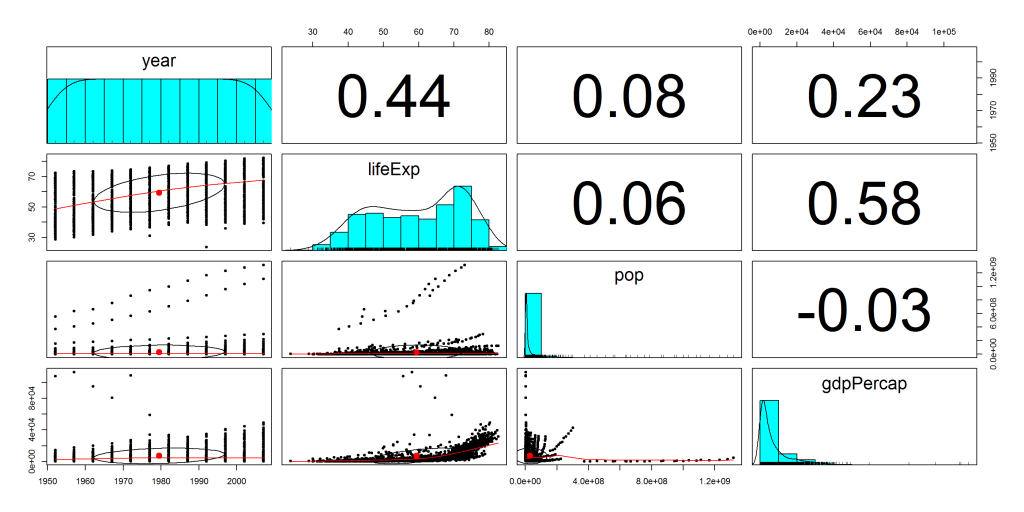
Ebenso eine weiter Darstellung der Korrelationen in einer visuell einfacheren Art und Weise.

Als letzte noch ein Beispiel einer SPLOM um weitere Darstellungsmöglichkeiten aufzuzeigen.

Schreibe einen Kommentar