Hierarchische Clusteranalyse

In diesem Artikel möchten wir die Hierarchische Clusteranalyse vorstellen.

Ist gibt zwei grundsätzliche Verfahren für die Hierarchische Clusteranalyse. Man nennt sie Top-Down und Bottom-Up Verfahren.

Die Top-Down Verfahren werden als divisive Cluster-verfahren bezeichnet. Im englischen Sprachgebrauch wird hierfür gerne die Abkürzung DIANA verwendet. Sie steht für Divise Analysis.

Wir steigen gleich ein, indem wir die notwendigen Bibliotheken laden:

library(tidyverse)  # data manipulation
library(cluster)    # clustering algorithms
library(factoextra) # clustering visualization
library(gapminder)

Verwendet wird in unserem Beispiel der gapminder Datensatz. Wir haben diesen bereits mit library(gapminder) geladen.

Betrachten wir den Datensatz mit der funktion head().

head()
A tibble: 6 x 6
 country        continent  year   lifeExp  pop        gdpPercap
                           
 1 Afghanistan  Asia       1952    28.8    8425333      779.
 2 Afghanistan  Asia       1957    30.3    9240934      821.
 3 Afghanistan  Asia       1962    32.0   10267083      853.
 4 Afghanistan  Asia       1967    34.0   11537966      836.
 5 Afghanistan  Asia       1972    36.1   13079460      740.
 6 Afghanistan  Asia       1977    38.4   14880372      786.

Der gapminder Datensatz zeigt die Entwicklungen der einzelnen Länder pro Jahr. Da wir Länder untereinander vergleichen möchten, werden wir mit Durchschnittswerten arbeiten. Diese erzeugen wir mit folgenden Code:

df <- gapminder %>% 
   group_by(country) %>%
   summarise(lifeExp_mean = mean(lifeExp), 
   pop_mean = mean(pop),      
   gdpPercap_mean = mean(gdpPercap)) %>%
   filter(lifeExp_mean < 50) %>% 
   na.omit()

head(df)

A tibble: 6 x 4
 country               lifeExp_mean  pop_mean         gdpPercap_mean
                                
 1 Afghanistan         37.5           15823715.           803.
 2 Albania             68.4            2580249.          3255.
 3 Algeria             59.0           19875406.          4426.
 4 Angola              37.9            7309390.          3607.
 5 Argentina           69.1           28602240.          8956.
 6 Australia           74.7           14649312.         19981.

Mit den nächsten Schritten werden wir die Daten anpassen, damit man eine Hierarchische Clusteranalyse durchführen kann. Zu Beginn werden wir die erste Spalte umwandeln, damit diese als Reihen namen erkannt wird.

df <-  column_to_rownames(df,"country")
 head(df)

                 lifeExp_mean      pop_mean            gdpPercap_mean
 Afghanistan     37.47883           15823715       802.6746
 Albania         68.43292            2580249      3255.3666
 Algeria         59.03017           19875406      4426.0260
 Angola          37.88350            7309390      3607.1005
 Argentina       69.06042           28602240      8955.5538
 Australia       74.66292           14649313     19980.5956

Danach folgt die Skalierung/Standardisierung der Daten mit scale().

df <- scale(df)
d <- dist(df, method = "euclidean")
head(d)

Nachdem die Skalierung / Standardisierung abgeschlossen ist, werden die Daten auf Unterschiede untersucht, bzw. es wird eine Distanzmatrix erstellt. Wir verwenden in unserem Beispiel den häufig verwendeten euklidischen Abstand. Wir haben die dist() funktion bereits oben ausgeführt.

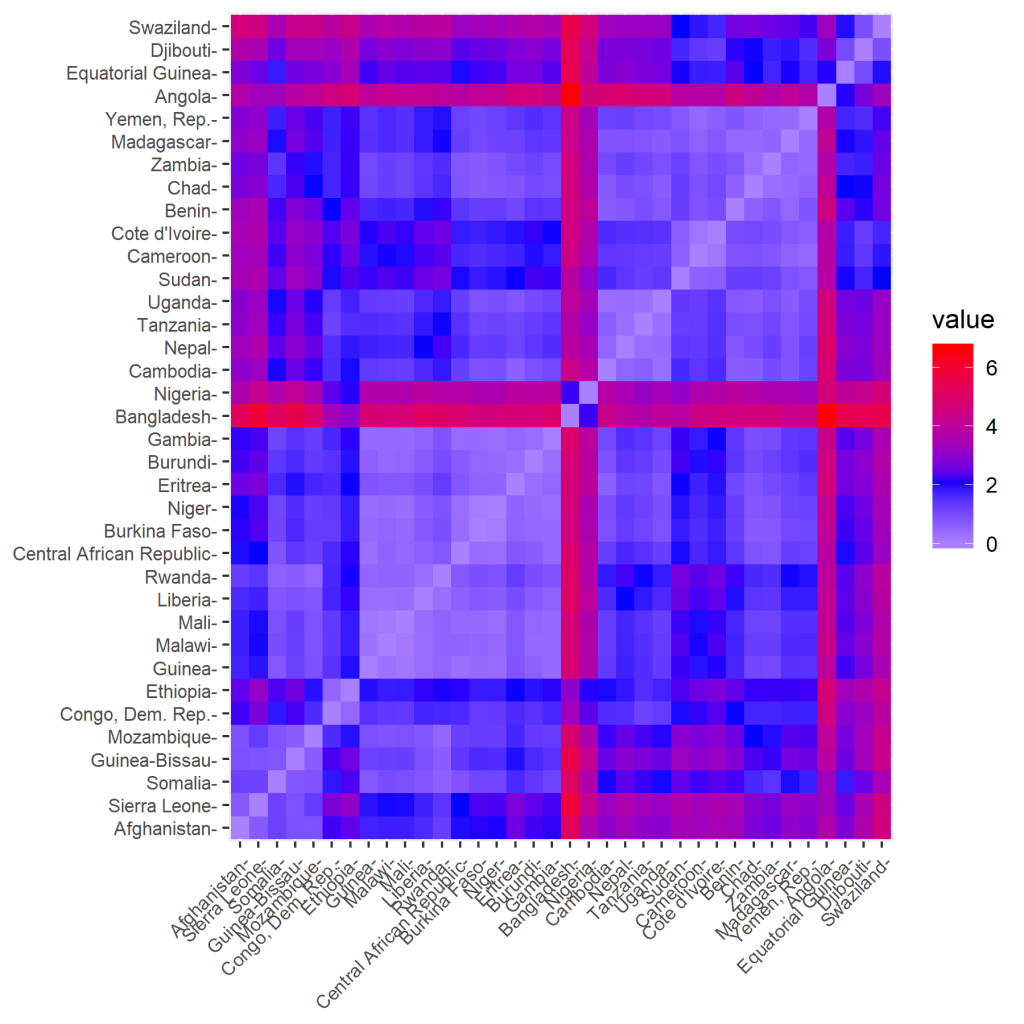
Die Distanzmatrix lässt sich auch bildlich darstellen. Wir verwenden dazu folgende Code:

fviz_dist(d, gradient = list(low = "white", mid = "blue", high = "red"))

Dadurch erhält man folgende Distanzmatrix als Bild:

Jetzt führen wir die Berechnung der Cluster durch. Dazu verwenden wir die „complete“ Methode.

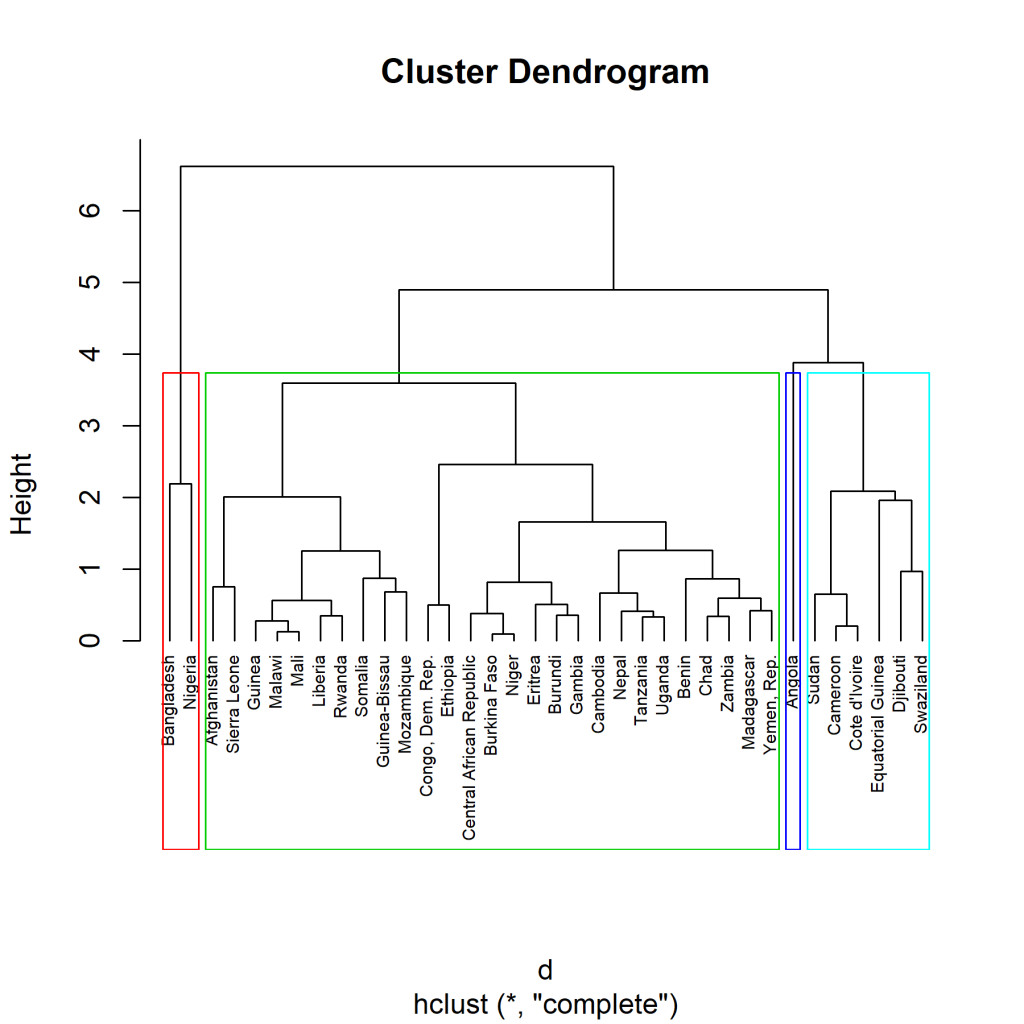
hc1 <- hclust(d, method = "complete" )
plot(hc1, cex = 0.6, hang = -1)
rect.hclust(hc1, k = 4, border = 2:6)

Mit der Funktion rect.hclust() haben wir die Cluster noch farblich in Quadrate eingeteilt.

Eine weitere Möglichkeit ist der Verwendung des factoextra Packetes. Wie führen den folgenden Code aus um das Paket zu verwenden:

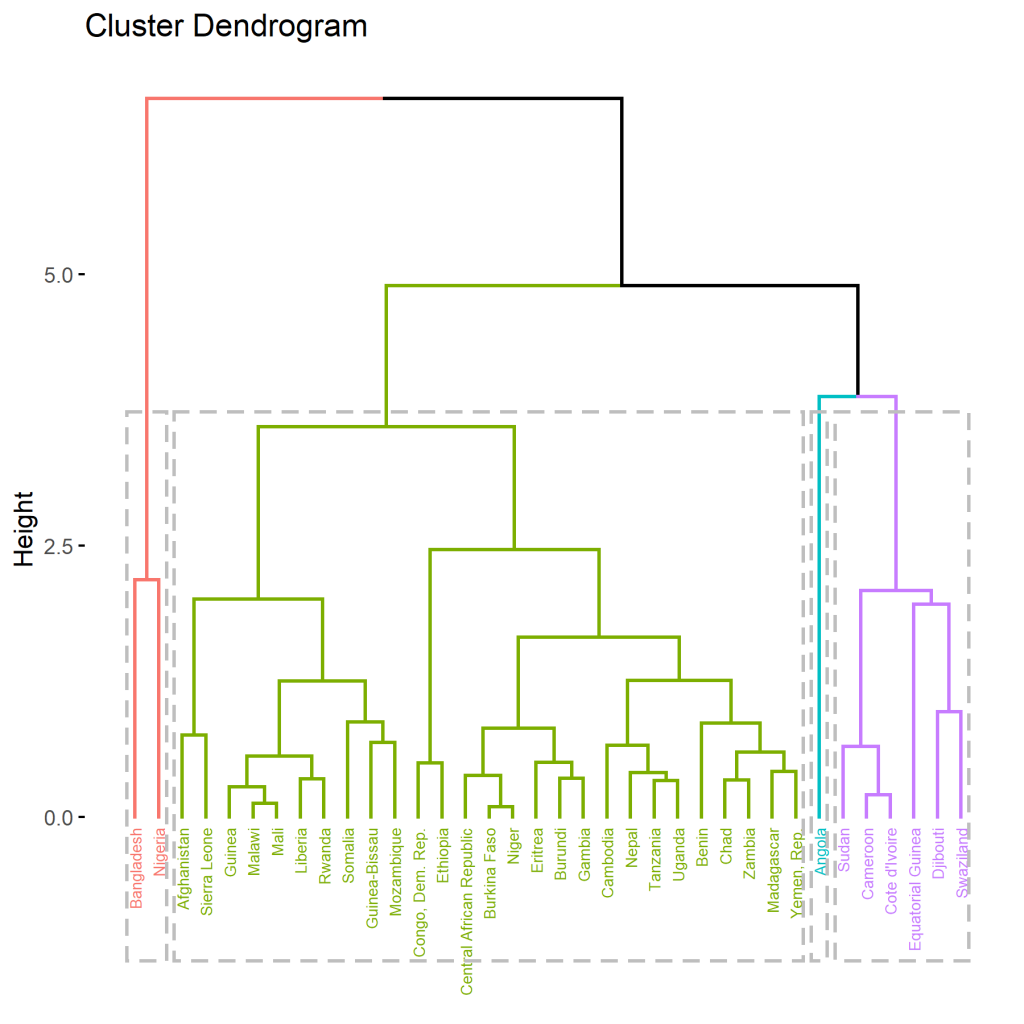
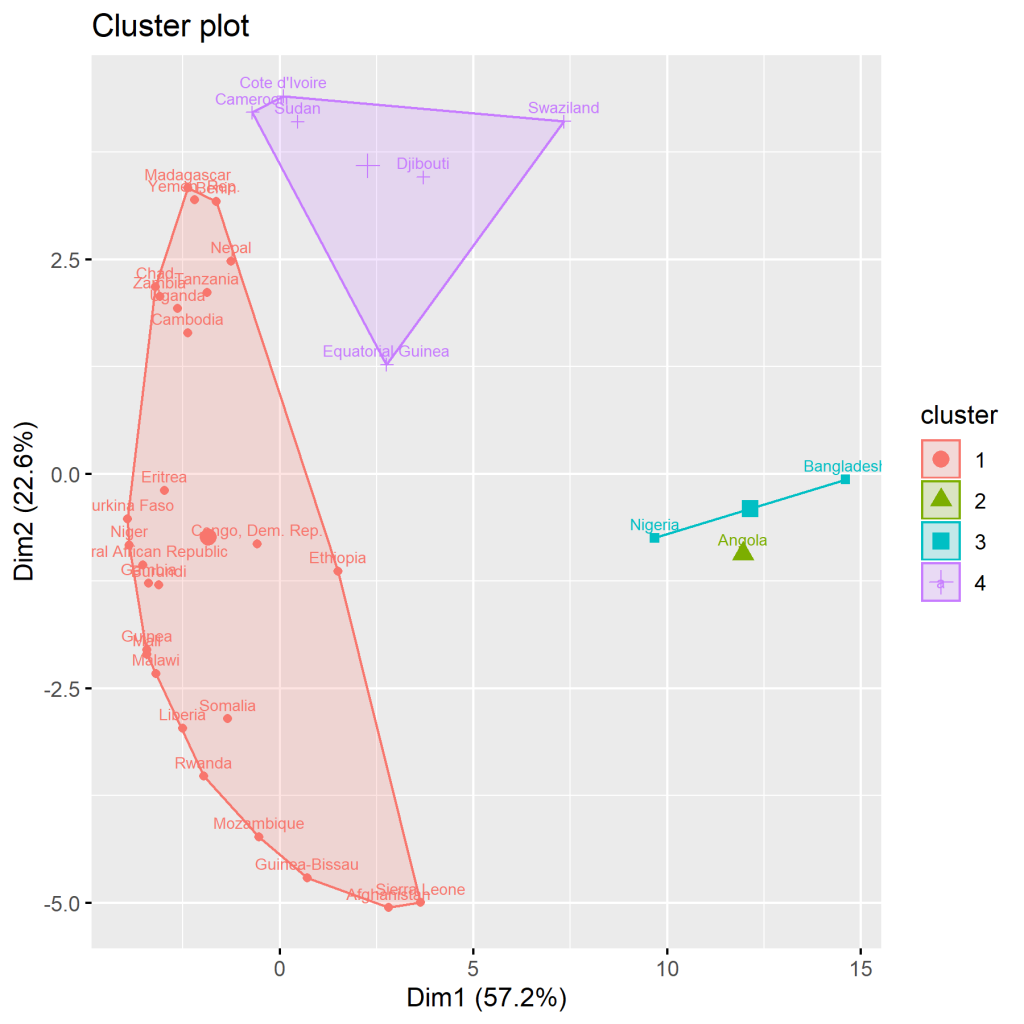
hc.cut <- hcut(d, k = 4, hc_method = "complete")
fviz_dend(hc.cut, show_labels = TRUE, rect = TRUE)
fviz_cluster(data=d,hc.cut, frame.type = "convex")

Erstell wird dadurch ein weiteres Dendrogramm und ein weitere Darstellung der Cluster.